Written by Chris Goodell, P.E., D. WRE | WEST Consultants
Copyright © RASModel.com. 2011. All rights reserved.
The traditional way of changing non-permanent ineffective flow areas to permanent involves going through each cross section, one at a time, in the cross section editor, selecting Options…Ineffective Flow Areas, and then manually checking which ineffective flow areas to make permanent.

This can be long and tedious if you have a lot of cross sections to change. HEC-RAS has an easy-to-use method for changing ineffective flow areas from non-permanent to permanent for multiple cross sections. In the geometry editor, select Tools…Ineffective Areas…Set to Permanent Mode.
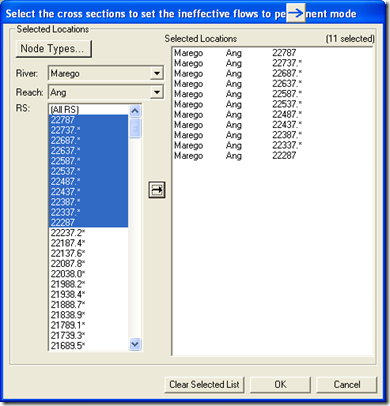
Here you select the cross sections with which you want to change the non-permanent ineffective flow areas to permanent, and RAS will do that for you. If you have a lot of cross sections where you want to do this, this utility is much faster than the traditional way of selecting each individual cross section in the cross section editor and manually changing the status.
There are a couple of disadvantages to the former method: First, with the traditional method, if you select a cross section to have its ineffective flow areas changed to non-permanent, all of the ineffective flow areas will be changed for that cross section. You cannot pick and choose within one cross section. Second, once you have changed a cross section’s ineffective flow areas to permanent, there is not a similar multiple cross section selection utility to go back to non-permanent.
Dr. Ray Walton, of WEST Consultants passed along a very easy way around this second disadvantage. First, open up the geometry file (*.g##) that you want to edit in a text editor. Wordpad, Notepad, WORD will all do. Go to the search tool and search on the string “ T”. That’s 7 spaces followed by a “T” which means “true”. This string is used in the text editor to indicate an ineffective flow area is permanent. Simply replace that text with “ F” (seven spaces followed by an “F”).
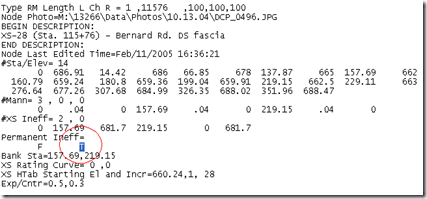
A simple “search and replace” action will allow you to make this change for a number of cross sections very quickly. If you have specific cross sections you wish to do this to, first search on the River Station. In the example above, the River Station is “11576”. Then scroll down to “ T” and change it to “ F”.
As always, be very careful when editing a RAS file directly in a text editor. It's very easy to corrupt the file if you make a small mis-type (i.e. you put in 6 spaces instead of 7 before the "F"). I always suggest making a copy of the original file for safe-keeping, before you make your edits.
Copyright © RASModel.com. 2011. All rights reserved.
The traditional way of changing non-permanent ineffective flow areas to permanent involves going through each cross section, one at a time, in the cross section editor, selecting Options…Ineffective Flow Areas, and then manually checking which ineffective flow areas to make permanent.

This can be long and tedious if you have a lot of cross sections to change. HEC-RAS has an easy-to-use method for changing ineffective flow areas from non-permanent to permanent for multiple cross sections. In the geometry editor, select Tools…Ineffective Areas…Set to Permanent Mode.

Here you select the cross sections with which you want to change the non-permanent ineffective flow areas to permanent, and RAS will do that for you. If you have a lot of cross sections where you want to do this, this utility is much faster than the traditional way of selecting each individual cross section in the cross section editor and manually changing the status.
There are a couple of disadvantages to the former method: First, with the traditional method, if you select a cross section to have its ineffective flow areas changed to non-permanent, all of the ineffective flow areas will be changed for that cross section. You cannot pick and choose within one cross section. Second, once you have changed a cross section’s ineffective flow areas to permanent, there is not a similar multiple cross section selection utility to go back to non-permanent.
Dr. Ray Walton, of WEST Consultants passed along a very easy way around this second disadvantage. First, open up the geometry file (*.g##) that you want to edit in a text editor. Wordpad, Notepad, WORD will all do. Go to the search tool and search on the string “ T”. That’s 7 spaces followed by a “T” which means “true”. This string is used in the text editor to indicate an ineffective flow area is permanent. Simply replace that text with “ F” (seven spaces followed by an “F”).

A simple “search and replace” action will allow you to make this change for a number of cross sections very quickly. If you have specific cross sections you wish to do this to, first search on the River Station. In the example above, the River Station is “11576”. Then scroll down to “ T” and change it to “ F”.
As always, be very careful when editing a RAS file directly in a text editor. It's very easy to corrupt the file if you make a small mis-type (i.e. you put in 6 spaces instead of 7 before the "F"). I always suggest making a copy of the original file for safe-keeping, before you make your edits.