Cross Section Points Filter

Written by Christopher Goodell, P.E., D.WRE  |  WEST Consultants

Copyright © The RAS Solution 2014.  All rights reserved.

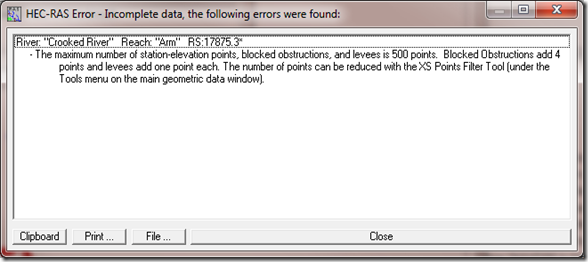
As RAS model development is done more and more through GIS, using the HEC-GeoRAS extension, cross section point filtering is becoming a standard part of the HEC-RAS model development exercise.  It’s not too uncommon for a model created in GIS to have multiple hundreds of cross section station elevation points.  This is normally not a problem, as long as you don’t exceed 500 points (the maximum allowed for any cross section in HEC-RAS.  However, do an interpolation with bounding cross sections that have more than 255 points each, and you will have interpolated sections with more than 500 points.  Try to run that model and HEC-RAS will give you a message like this:

Fortunately, this is easily remedied.  Simply use the Cross Section Points Filter tool located in the Tools menu item in the Geometry schematic:

In this tool, you can filter a single cross section, or do multiple cross sections together.  For a single cross section, either go to the cross section indicated in the error message, or scroll through the river station dropdown box until you find one with more than 500 points.

Once you’ve selected your cross section(s), you have a number of different ways to filter.  Near and Colinear filtering will remove points that are either very close to another point, or that are in line with other points.  You just provide the tolerances (tell RAS how close is too close, etc.) . Once you enter the tolerance values, press the “Filter Points on Selected XS”, and check to see if you removed enough points to get below 500.  If not, you’ll have to tighten your tolerances.  This can take a little bit of trial and error as you figure out what tolerance levels will remove enough points. 

My preferred method for filtering is to use the “Minimum Area Change” method.

Here, all you do is enter in the desired number of cross section points you wish to have in the cross section (500 or less), and then HEC-RAS will remove points until it gets to that number.  No trial and error necessary.  BUT, you do not have control on which points are removed.  HEC-RAS uses a built-in scheme to remove points while minimizing the change in cross section area.  At first I was a bit reluctant to use this feature, thinking that it might drastically alter the shape of my cross section.  However, when comparing the original and filtered cross sections, I’ve never noticed a visual difference.  The “minimum area change” scheme that is used by HEC-RAS does a very good job at preserving the shape and hydraulic characteristics.  Give it a try next time you need to filter. 

Software to check downstream boundary conditions.

Although I don't typically use The RAS Solution to promote software other than HEC-RAS, this utility by Mr. Vladimir Moya is free and some of you may find it useful for testing the effects of different boundary conditions in steady flow, when using normal depth.  Enjoy!

http://sciengsustainability.blogspot.jp/2014/02/boundary-conditions-in-hec-ras.html

Vertical Datum Adjustments in HEC-RAS

Written by Daniela Todesco, P.E.  |  WEST Consultants

Copyright © The RAS Solution 2014.  All rights reserved.

If you have built enough HEC-RAS models, you’ve probably discovered that having data in different vertical datums is a bit of a pain. RAS lets you adjust the vertical datum of individual cross sections (under “Geometric Data”, “Cross Section”, “Options”, “Adjust Elevations”) or portions of the model (“Geometric Data”, “Tools”, “Datum Adjustment”). However, I have to confess this: datum adjustments are always a little bit puzzling to me. I need pen and paper and a little numbering conversion to make sure that I’m doing things right when moving from one vertical datum to the next. And I recently had a “eureka” moment when I finally realized that the sentence “NAVD88 is higher than NGVD29 (for most of the locations we work on)” is actually wrong. Let me step back a moment and I’ll explain why.

The two most common vertical datums used in the U.S. are the North American Vertical Datum of 1988 (NAVD88) and the National Geodetic Vertical Datum of 1929 (NGVD29). NOAA’s VERTCON program can be used to compute the conversion factors from one datum to the other.

Tidal datums are, in general, confusing. Vertical elevations can refer to NAVD88, the station datum, Mean High Water, Mean Low Water, Mean Range of Tide, and a variety of other datums. In recent years, NOAA has been updating its reference tables with excellent graphs showing how the different datums relate to each other (like the one below for Astoria, OR - http://tidesandcurrents.noaa.gov/datums.html?id=9439040 -, where all elevations presented are related to the station datum, which is the Columbia River Datum or CRD).

Let’s say that you download data in the Astoria station datum and you want to convert the data in NAVD88. Since the NAVD88 datum is 2.02 ft above the station datum, you need to subtract 2.02 ft from the station datum to obtain elevations in NAVD88. Or, to make it easier to remember, if the data you obtain is in datum X and you want to convert it to datum Y, you need to ADD the vertical distance between the two datums if X is ABOVE Y (or SUBTRACT if X is below Y). In our case, X is the Astoria station datum, Y is NAVD88, X is below Y, and you subtract 2.02 ft to the Astoria datum to obtain elevations in NAVD88 (the distance between the two). Makes sense, right? This also explains why for most locations on the West Coast USA, the elevation in NAVD88 of a certain location is always higher than the elevation in NGVD29 of the same location (that’s because the NGVD29 datum is actually above the NAVD88 datum). For example, in Astoria, you need to subtract 3.4 ft to elevations in NAVD88 to obtain elevations in NGVD29.

Now, to confuse things even more, gage locations along the Columbia River follow an intrinsic datum that actually changes as you move upstream from the river’s mouth. For example, at Astoria, the station datum is BELOW NGVD29, while at Vancouver, the station datum is ABOVE NGVD29 (see graph below, at http://www.thsoa.org/hy05/09_1.pdf).

The USGS sent us a nice graph (see below) that helped me clear things up when reading datum-related station description information. This one is for the Columbia River at Vancouver gage in WA. The short station description reads: “Datum of gage: 1.82 ft above NGVD29”. The long version reads: “Datum of gage is Columbia River Datum (add 1.82 ft to correct to NGVD29)”. Remember: X is the station datum, Y is NGVD 29, X is ABOVE Y, so you need to add the distance to go from X to Y. To add something more to this graph, I would say that in CRD, the 0 of the NGVD29 datum is 1.82 ft below the 0 of the CDR datum, which reflects the previous graph. Hope this helps!

Lateral Structure Coefficients

Written by Chris Goodell, P.E., D.WRE  |  WEST Consultants

Copyright © RASModel.com.  2013.  All rights reserved.

Lateral structures can be used in HEC-RAS to transfer flow from a river/reach to a storage area, or to another river/reach.  With the coming release of HEC-RAS with 2D capabilities (estimated beta release January/February 2014), you’ll be able to hook a river/reach to a 2-D area using a lateral structure. 
Although its primary function in HEC-RAS is to transfer flow out of one river/reach into another component (river/reach, storage area, 2D area), a lateral structure can physically represent a wide range of geometric features, including a levee, a flow diversion structure, a morning glory spillway, or even a natural ground or bathymetric profile.  Including a lateral structure in your model to represent a levee is important if the levee is ever overtopped or breached during the simulation.  Flow diversion structures can have multiple outlet features, including culverts, gates, and spillways.  These features are all available in the lateral structure editor in HEC-RAS. 
Another common use of lateral structures is to simulate flow transfer from the river to a tributary during a flood event.  This is especially convenient if you don’t want to model the tributary as an individual reach, but still want to account for it’s available storage, for a proper accounting of flood wave attenuation in the main stem river/reach.  As an example, the following figure shows a storage area representing a tributary to the main stem river.  This storage area is connected to the main stem by a lateral structure (highlighted in red). 

Because a lateral structure can represent a variety of different flow transferring structures (or non-structures), the hydraulics in and around the lateral structure can be quite different, depending upon the case.  Every lateral structure in HEC-RAS requires a lateral weir coefficient, and different hydraulics mean different lateral weir coefficients.  Any hydraulics textbook will have a multitude of weir coefficients for “inline” conditions, but it’s rare to find something similar for lateral flows, or diversion flows.  But it is generally agreed that lateral structure weir coefficients should be much lower than a similar inline configuration.  For example, an inline, hydraulically efficient broad-crested weir might have a weir coefficient around 3.0 (US units) or 1.7 (SI Units).  Turn that structure sideways (a lateral structure), and it will have a coefficient closer to 2.0 (US Units) or 1.1 (SI Units).  The difference is due to the energy/momentum loss associated with turning flow lines from their downstream orientation to a lateral direction out of the river/reach.    Unfortunately, there has simply not been a lot of research done on quantifying this energy/momentum loss and what that does to lateral weir coefficients.
The research that is available could be useful and might be worth checking out.  Hagar’s equation is one reference and is actually built into the HEC-RAS lateral structure editor, under Lateral Weir Embankment…Weir Computations.  It will compute an equivalent lateral weir coefficient based on an inline value (the Default Weir Coefficient) and some physical and hydraulic properties of the weir and  the adjacent river/reach. 

You can read more about Hagar’s equation in the HEC-RAS Hydraulic Reference Manual on page 8-17. 
Useful references for lateral structure weir coefficients (including Hager’s):

• Hager, W.H. (1987). “Lateral Outflow over Side Weirs.” Journal of Hydraulic Engineering, ASCE, 113(4).
• Borghei, S.M.; Malili, M.R.; Ghodsian, M. (1999). “Discharge Coefficient for Sharp-Crested Side Weir in Subcritical Flow.” Journal of Hydraulic Engineering, ASCE, October, 1999.
• Ranga Raju, K.G.; Prasad, B.; Gupta, S.K. (1979). “Side Weir in Rectangular Channel.” Journal of Hydraulic Engineering, ASCE, 105(5).
• Subramanya, K.; Awasthy, S.C. (1972). “Spatially Varied Flow over Side Weirs.” J. Hydr. Div., ASCE, 98(1).
• Singh, R.; Manivannan, D.; Satyanarayana T. (1994). “Discharge Coefficient of Rectangular Side Weirs.” Journal of Irrigation and Drainage Engineering, ASCE, 120(4).

However, none of these references discuss lateral weir coefficients for lateral flow transfers over natural ground, or surface flow (i.e. non-elevation overbank terrain).  HEC has a reference table for lateral structure coefficients that I like to use-it’s also included in the new “Combined 1D and 2D Modeling with HEC-RAS” document that was released in August 2013, in anticipation of the new 2D feature in HEC-RAS expected to be released as a beta version in the January/February 2014 time frame.   Note how low the suggested range of coefficients is for “non-elevated overbank terrain.”  Because they are not dimensionless, be aware that weir coefficients in SI Units are different from US units by a factor of the square root of the ratio of the SI gravitational constant to the US gravitational constant,

What is being modeled with the Lateral Structure	Description	Range of Weir Coefficients
Levee/Roadway – 3 ft (1 meter) or higher above natural ground	Broad crested weir shape, flow over Levee/road acts like weir flow	US Units: 1.5 to 2.2 (2.0 default) SI Units:  0.83 to 1.2 (1.1 default)
Levee/Roadway – 1 to 3 ft (0.3 to 1.0 meter) elevated above ground	Broad crested weir shape, flow over levee/road acts like weir flow, but becomes submerged easily.	US Units:  1.0 to 2.0 SI Units:  0.55 to 1.1
Natural high ground barrier – 1 to 3 ft (0.3 to 1.0 meter) high.	Does not really act like a weir, but must flow over high ground to get into 2D (or storage) area.	US Units: 0.5 to 1.0 SI Units: 0.28 to 0.55
Non-elevated overbank terrain. Lateral Structure not elevated above ground	Overland flow escaping the main river.	US Units: 0.1 to 0.5 SI Units:  0.06 to 0.28

*Hydrologic Engineering Center, August 2013.  “Combined 1D and 2D Modeling with HEC-RAS”

Although this table is presented within the context of 1-D to 2-D flow transfers, these values will work with river/reach to storage area or river/reach to river/reach flow transfers as well.  As noted in the referenced document (HEC 2013), “In general, Lateral Structure weir coefficients should be lower than typical values used for inline weirs.  Additionally, when a lateral structure (i.e. weir equation) is being used to transfer flow from the river (1D region) to the floodplain (2D Flow Area), and then [sic] the weir coefficients that are used need to be very low, or too much flow will be transferred.”  Also, “The number 1 problem people have been having with interfacing 1D river reaches with 2D areas, is user’s [sic] have been using way to [sic] high of weir coefficients for the situation being modeled.  If the lateral structure is really just an overland flow interface between the 1D river and the 2D floodplain, then weir coefficients in the range of 0.1 to 0.5 must be used to get the right flow transfer and keep the model stable.” 

The HEC 2013 document ("Combined 1D and 2D Modeling with HEC-RAS") with the Table of lateral weir coefficients can be downloaded from my Google Drive site here:  https://drive.google.com/file/d/0B_s8OLJOgOi0Nm5sdHFhSzFUYkk/edit?usp=sharing.  The lateral weir coefficient table is on page 35.

Filtering Station Elevation Data in HEC-RAS

Written by Daniela Todesco | WEST Consultants
Copyright © RASModel.com. 2013.  All rights reserved.

I am working on a dam breach project where I’m trying to simplify a complicated model with dozens of tributaries and storage areas. In the process, I’m converting a few tributaries into storage areas (which are surrounded by other storage areas). For example, I want to convert the reach below (from 5.43 to 0.55) to a storage area. We happen to have the topographic data used to generate the original model (although we don’t have the original geodatabase), so we’re good to go. In order to do that, we need to delineate the storage area polygon, define new storage area connections, and generate lateral structures. The new “reach” (now a storage area) will look like the one below. Now we need station-elevation data for storage area connections and lateral structures. Easy, right? Well, not so fast. HEC-GeoRAS seems to have some issues exporting data when you take an existing project and try to modify shapefiles and extract data for only a portion of the entire model. It is especially difficult if you’re not the one who built the model in the first place. The shortcut is to think outside GeoRAS and obtain simple 3D station-elevation points directly from a TIN or grid for the storage area or structures you need. The bad part about that is that extracting tools in ArcGIS doesn’t really have an option to limit the number of points that are generated, and you end up with thousands of points that you can’t really use in HEC-RAS (the limit for cross section points, storage area connection weir/embankment points, and lateral structure weir points is 500). For example, in the connection called 83Coal in the figure above, I end up with over 2300 points. I’m stuck. Or so I thought… It turns out that RAS automatically “expands” its Station Elevation table to store however many points you need. In my case, 2339… HEC-RAS will still give you an error if you try to run the model with this data (the limit of 500 points still stands for computations!), but a simple click of the “Filter” button you see in the figure above solves the problem. Voila! Hope you liked this new (for me) discovery.

Stabilizing a Dynamic Unsteady HEC-RAS Model

Written by Chris Goodell
Copyright © RASModel.com. 2013.  All rights reserved.

One of the most frustrating aspects of unsteady HEC-RAS modeling can be the model stabilization process. You know, you’ve gone to great lengths collecting the best survey/topo data and solid hydrology. Then you’ve painstakingly spent hours…possibly days entered all of that data only to find that once you press the “Compute” button, the model crashes. The dreaded “Red Bar”! Sometimes you can get your simulation to complete without crashing, but the listed numerical errors are so high that you can’t with good conscience submit that as your final simulation. Either way, approaching an unsteady HEC-RAS model (especially a dynamic one) as a beginner with little experience and understanding of how to stabilize it can cause significant delays in your project and worse, completely blow up your budget. I’ve uploaded two HEC-RAS projects to the following Google Drive Site: https://drive.google.com/folderview?id=0B_s8OLJOgOi0YU92SGZQZm9raWM&usp=sharing



RawleyResUnstable.prj is an unsteady flow dam breach HEC-RAS project recently sent to me for help. Although the model ran to completion without crashing, it had unacceptably high errors.
RawleyResStable.prj is the fully stabilized version of the model with no numerical errors.

The following lists out the courses of action taken to stabilize the model. Feel free to download the “Unstable” and “Stable” models and try these techniques on your own. The links following some of these items will take you to more information about that particular technique.

1. Cross Section Spacing. The initial spacing was way too coarse. A visual check alone of the geometry schematic and profile plot should encourage you to investigate a finer cross section spacing.

Geometry Schematic

Profile Plot Samuels equation suggests anywhere from 15 ft to 50 ft spacing (depending on what bed slope you use). I interpolated to 50 ft for the entire reach. http://hecrasmodel.blogspot.com/2008/12/samuels-equation-for-cross-section.html

2. Dam Breach models typically have time steps on the order of a minute or less. This model was initially set with a computation interval of 10 minutes which is high even for the largest and “slowest” of dam breach models. I changed the time step to 10 seconds. The selection of 10 seconds was based on “gut” feel and lots of experience doing dam breach models. There are some methods for approximating good timesteps, notably the Courant Condition and Fread’s equation. Also, setting the cross section spacing/timestep ratio equal to a representative stream velocity will get you close. In this case, the cross section spacing is 50 ft, and I was able to pull some velocities (prior to the model crashing) at about 6 ft/s. That suggests a time step of 8.3 seconds. Close enough to 10 seconds, so we’ll stick with that.

3. I changed the downstream boundary normal depth slope from 0.01 to 0.001. Not sure what is downstream of the first cross section, but 0.01 is awfully steep and was setting up a very low depth at the downstream boundary (which was causing instabilities). http://hecrasmodel.blogspot.com/2010/01/downstream-boundary-normal-depth.html

Notice in the following profile plot of the downstream end of the reach how the water surface at the boundary cross section is below critical depth (the red dot). This creates an overestimation of the water depth at the next upstream cross section, which in turns creates some instability over the next several timesteps.

The proper way to handle this would be to find out what is downstream of your model and select a boundary condition that best represents those conditions. In absence of downstream conditions, the 0.001 slope for normal depth provides a reasonable solution.  Either way, this underscores the importance of moving your downstream boundary far away from your area of interest in your study reach.  That way the errors that do originate from your downstream boundary assumption will have diminished to negligible levels before impacting your area of interest. 

4. In the unsteady flow editor, the initial flow and the first time step flow should always be equal. In the original model, the initial flow is left blank (which is actually okay because RAS will use the first timestep flow if left blank). However, the first time step flow is very low at 0.14 cfs. Peak discharge of your inflow hydrograph is around 600 cfs. I put in a baseflow (minimum flow) of 5% of this, which is 30 cfs. Just to be safe, I put 30 cfs in the initial flow input box as well. It’s important to make sure that the 30 cfs baseflow does not have an impact on the peak of the breach outflow hydrograph. http://hecrasmodel.blogspot.com/2009/02/minimum-flow-requirements.html

5. The upstream end of your reservoir is very steep (14%). This one was easy to spot in the profile plot because of the very nice smooth profile plot followed by a sudden spike in the energy level (green dashed line) at the upstream end. Notice to that there is a corresponding supercritical solution at the upstream most cross section. These are both indications that more cross sections are needed here. http://hecrasmodel.blogspot.com/2010/01/another-reason-for-interpolated-cross.html

I added more cross sections by interpolating the steep slope at the upstream end of the reservoir (10 ft spacing).

Notice the energy spike is not completely gone, but it is much better. Refining the HTAB parameters (http://hecrasmodel.blogspot.com/2009/02/crazy-energy-grade-line.html), turning on mixed flow and bumping up n values will collectively take care of the rest of this (see numbers 8, 9, and 10 below).

7. From RS 4577 to 3791 you have your main channel defined in a small elevated side channel. The right overbank is lower in elevation than the channel.

This is problematic in RAS. Using the graphical cross section editor, I redefined the bank stations to get rid of this problem.

8. Notice now in the HTAB parameters property table, the HTAB definition begins at the elevation of the invert of the side channel that was previously defined as the main channel. There is a big gap in the computation points in the newly defined main channel. This poses problems with HEC-RAS, particularly at low discharges/stages, since RAS will have to extrapolate to obtain a solution over that range.

I readjusted the cross section HTAB parameters to reflect the new bank station definitions (I used the “Copy Invert” button for all cross sections). While in there, I maximized the resolution of the HTAB parameters by changing number of points to 100 and minimizing the increment as much as possible while still having full coverage of each cross section. http://hecrasmodel.blogspot.com/2009/02/crazy-energy-grade-line.html http://hecrasmodel.blogspot.com/2011/03/more-on-htab-parameters.html

9. In the figure below, notice all of the “red” areas in this zoomed in section of the  upstream end of the reach.

These are areas that are near critical depth. I turned on the “Mixed Flow” option in the Unsteady Flow Analysis window, which helps stabilize the near critical depths at the upstream end of the reservoir. http://hecrasmodel.blogspot.com/2011/04/mixed-flow-regime-options-lpi-method.html If you’ve been following along correcting your own copy of the model, you’ll notice that the model now finally runs to completion without crashing. There are still a few minor errors as shown in the Computation Messages.

It’s debatable whether you need to take care of these relatively small errors. Particularly for a dam breach model, where the presumed errors of the input data probably far outweigh these small numerical errors. Nevertheless, there’s a sense of pride in putting out a very robust model, completely free of numerical errors. So…let’s continue.

10. The errors in the computation window above suggest a problem around river station 6200. That happens to be the upstream end of the reservoir and the source of the error can clearly be seen with the energy grade line and critical depth turned on.

The section at the upstream end of the reservoir is very steep at about 13.5%. In fact, that’s greater than the suggested maximum slope of 10%, as stated in the HEC-RAS manuals. You can see as the pool starts to lower, the steep reach is exposed and because of the low n values, the water surface is calculated to be supercritical. Let’s assume that the geometry is correct, and the upstream end of the reservoir really is that steep. Jarrett’s Equation suggests very high n values should be used here (~0.2), based on the bed slope and hydraulic radius (after the breach when the reservoir has drained). The original model had 0.07 and 0.035 for the overbanks and main channel, respectively. I changed all the n values in this steep reach to 0.15, because I think 0.2 might be a little overkill. http://hecrasmodel.blogspot.com/2009/12/n-values-in-steep-streams.html

There…no errors! However, there is still a Warning about extrapolating above/beyond the rating curve at a bridge (R.S. 277).

11. To get rid of that warning, I increased the HTAB headwater maximum elevation at River Station 277 (the bridge) from 278 ft to 280 ft so that RAS doesn’t have to extrapolate.

There we have it. A clean solution. No errors, no warnings.

Downstream Boundaries

Written by Chris Goodell | WEST Consultants
Copyright © RASModel.com. 2013.  All rights reserved.

I just received this question about downstream boundaries in HEC-RAS, and thought it would make a nice post here on RASModel.com.

"...regarding the boundary condition, if I use critical depth instead of normal depth will it be unacceptable?  When choosing the normal depth I need to enter a slope, can i use just one slope for the whole stream?"

Either critical or normal depth will work fine IF they are far enough downstream from your area of interest.  Normal depth is usually better, because it is typically a better representation of actual stream conditions.  Critical depth is only accurate when used at a significant grade break, a drop structure, a waterfall, etc., where flow passes through critical depth.  Critical depth does not happen in natural streams very often, and usually the water depth is nowhere near critical depth.  Using critical depth for a typical section of natural river is wrong.   That’s why I tend to always use normal depth.  However, using critical depth as a boundary condition is convenient (it’s easy to use, right?!?!), so it does have some merit. 

For normal depth, the slope you enter is not the slope of your modeled reach.  It represents the slope of the reach downstream of your downstream-most cross section.  You can often times approximate this slope by using a topographic map and locating where topo lines cross the stream, then measure the streamwise distance between them.  But remember this should be done DOWNSTREAM of your downstream cross section.  Normal depth as a boundary condition in RAS is applied to one cross section only-the downstream cross section, and using it means you are assuming that the reach just downstream of your downstream cross section is flowing under uniform (normal) conditions.  This too, is almost never the case in a natural stream due to the constant variation of cross section size and shape.  However, it is much closer to the true solution than critical depth is. 

The bottom line is both methods (in fact ALL methods) for assigning a downstream boundary have some inaccuracies.  That is why it is important to maintain distance between your downstream boundary and the area of your model that you are interested in.  One of the great things about the solution scheme in HEC-RAS is that it is "self-healing".  In other words, if there is an error at a specific location (due to a bad boundary condition, improper n value, poor survey data, that error will diminish the further away from that location you move.  At some point upstream, the effect of that error will no longer be "felt".  How far downstream you need to place the downstream boundary is variable, but you can test this by trying different downstream boundary assumptoins (critical depth and normal depth, or simply normal depth with a bunch of different normal slope assumptions) and seeing how far upstream you need to be to not see an effect from different downstream boundary assumptions.  This post demonstrates this technique:  http://hecrasmodel.blogspot.com/2010/01/downstream-boundary-normal-depth.html