Written by Chris Goodell, P.E., D. WRE | WEST Consultants
Copyright © RASModel.com. 2012. All rights reserved.
A very convenient way to troubleshoot instability problems with very complex models is the use of a hotstart run with a stepdown scheme. Creating a stepdown scheme hotstart plan is covered in detail here. In a previous post, I explained some problems with running the stepdown scheme when you have bridges. Here I want to highlight problems you may run into with cross sections while running the stepdown scheme.
While drowning out the entire model to provide a high degree of numerical stability, you will be exceeding the maximum HTAB computation points, sometimes by several hundred feet/meters or more. Technically, this is okay, since HEC-RAS will extrapolate the HTAB curves as needed. However, extrapolation is done linearly off the last two HTAB points on the computed curve. If the last two points of the curve happen to be at a location of discontinuity on the curve, bad things can happen. Take for instance this computed HTAB curve of Conveyance vs. Stage:

It looks pretty good. However, if you zoom in on the end point, you can see that there is a discontinuity in the curve.

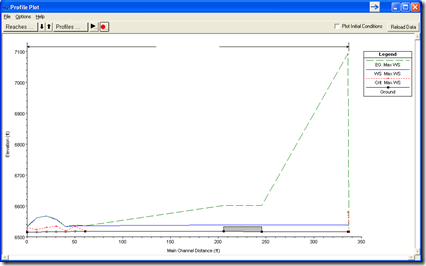
Not a big deal, since normally we are well below the last point on the HTAB plots. However if you are running a step-down scheme, RAS will have to extrapolate off of the last two points when the model is “drowned” and you can see that there will be an overestimation of water surface elevation at the subject cross section during the stepdown process as shown below in the profile plot. If the overestimation of stage is severe enough, the resulting “stairstep” could lead to numerical instability, causing your model to crash.
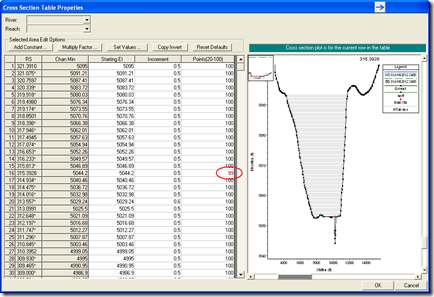
A quick fix to this problem is to just slightly change how the HTAB curves are constructed for the problem cross sections. Simply remove the last point in the curve by reducing the number of points in the Cross Section Table Properties by 1 (in the example below, change 100 to 99).
This will provide a much better linear extrapolation and get rid of the “stairstep” problem in the stepdown scheme.

Of course a “seasoned” RAS modeler will recognize what is causing the discontinuity in the HTAB curve in the first place and could eliminate that problem by fixing the geometry, whether it be better definition of ineffective flow areas, levee markers, n-value breakpoints, etc. However, the savvy modeler would recognize that the discontinuity exists at the end points of the cross section, well above the normal water surface elevation range. Once the model is stable, there’s no need to spend time fixing this.
Copyright © RASModel.com. 2012. All rights reserved.
A very convenient way to troubleshoot instability problems with very complex models is the use of a hotstart run with a stepdown scheme. Creating a stepdown scheme hotstart plan is covered in detail here. In a previous post, I explained some problems with running the stepdown scheme when you have bridges. Here I want to highlight problems you may run into with cross sections while running the stepdown scheme.
While drowning out the entire model to provide a high degree of numerical stability, you will be exceeding the maximum HTAB computation points, sometimes by several hundred feet/meters or more. Technically, this is okay, since HEC-RAS will extrapolate the HTAB curves as needed. However, extrapolation is done linearly off the last two HTAB points on the computed curve. If the last two points of the curve happen to be at a location of discontinuity on the curve, bad things can happen. Take for instance this computed HTAB curve of Conveyance vs. Stage:

It looks pretty good. However, if you zoom in on the end point, you can see that there is a discontinuity in the curve.

Not a big deal, since normally we are well below the last point on the HTAB plots. However if you are running a step-down scheme, RAS will have to extrapolate off of the last two points when the model is “drowned” and you can see that there will be an overestimation of water surface elevation at the subject cross section during the stepdown process as shown below in the profile plot. If the overestimation of stage is severe enough, the resulting “stairstep” could lead to numerical instability, causing your model to crash.

A quick fix to this problem is to just slightly change how the HTAB curves are constructed for the problem cross sections. Simply remove the last point in the curve by reducing the number of points in the Cross Section Table Properties by 1 (in the example below, change 100 to 99).

This will provide a much better linear extrapolation and get rid of the “stairstep” problem in the stepdown scheme.

Of course a “seasoned” RAS modeler will recognize what is causing the discontinuity in the HTAB curve in the first place and could eliminate that problem by fixing the geometry, whether it be better definition of ineffective flow areas, levee markers, n-value breakpoints, etc. However, the savvy modeler would recognize that the discontinuity exists at the end points of the cross section, well above the normal water surface elevation range. Once the model is stable, there’s no need to spend time fixing this.
















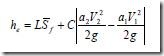
![clip_image002[4] clip_image002[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhQdLG_hTEqkxyxlw5HXlyPRcj2u4zoXXQ2BjJoEEjkiwtZ_hXmu_x2nsLqCe_Y-yVHm9mqtys_cUkWE1osh8nR-KbEBglVcODu86OKm1rCG0Cyf4fOlOgGFtvlaiywOjgnJZIhX2aQeERW/?imgmax=800)





